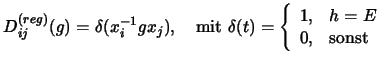Nächste Seite: Charaktere
Aufwärts: Wichtige Begriffe und Definitionen
Vorherige Seite: Reduzibilität
Bei der regulären Darstellung handelt es sich um eine besondere Darstellung, die
sich bei gegebener (endlicher) Gruppe sehr einfach konstruieren läßt:
Im folgenden bezeichnen 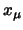 die in beliebiger, aber fester Reihenfolge
durchnummerierten Elemente der Gruppe
die in beliebiger, aber fester Reihenfolge
durchnummerierten Elemente der Gruppe 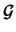 ,
, 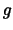 ein beliebiges Element der Gruppe.
Dann definiert man:
ein beliebiges Element der Gruppe.
Dann definiert man:
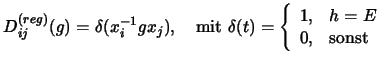
Es gilt offensichtlich:
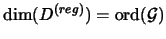 .
.
Bei dieser Konstruktion kann man die kanonische Basis des Vektorraumes mit den
Gruppenelementen (in der gegebenen Reihenfolge) interpretieren. Dann wirken die
dargestellten Gruppenelemente so auf die Basisvektoren, wie es durch die
Gruppenmultiplikation in 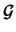 induziert wird; d.h., der
induziert wird; d.h., der 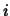 -te Basisvektor
wird unter Anwendung von
-te Basisvektor
wird unter Anwendung von 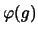 zu dem Basisvektor, der
zu dem Basisvektor, der 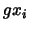 entspricht.
entspricht.
Martin Rehwald
1999-10-27