Next: Mixed derivatives Up: Finite difference method Previous: Finite difference method
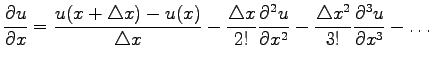 |
(1.2) |
is called a forward difference. The backward expansion of the function
is called a backward difference. if we substract Eq. (1.5) from Eq. (1.3) one obtains
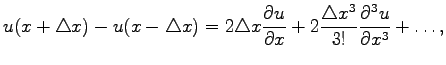 |
(1.6) |
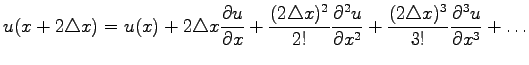 |
(1.8) |
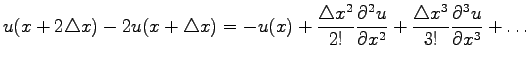 |
(1.9) |