Linear Second-Order PDEs

For linear equations in two dimensions there is a simple classification in terms of the general equation

$$au_{xx}+bu_{xy}+cu_{yy}+du_x+eu_y+fu+g=0,$$

where the coefficients $a,b,c,d,e,f$ and $g$ are real and in general can also be functions of $x$ and $y$ . The PDE's of this type are classified by value of discriminant $D_{\lambda}=b^2-4ac$ of the eigenvalue problem for the matrix

$$A=\begin{pmatrix} a & b/2\\ b/2 & c \end{pmatrix},$$

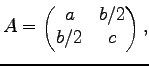
build from the coefficients of the highest derivatives. A simple classification is shown on the following table:

$D_{\lambda}$	Typ	Eigenvalues
$D_{\lambda}<0$	elliptic	the same sign
$D_{\lambda}>0$	hyperbolic	different signs
$D_{\lambda}=0$	parabolic	zero is an eigenvalue

For instance, the Laplace equation for the electrostatic potential $\varphi$ in the space without a charge

$$\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}=0$$

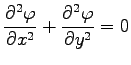
is elliptic, as $a=c=1$ , $b=0$ , $D_{\lambda}=-4<0$ . In general, elliptic PDEs describe processes that have already reached steady state, and hence are time-independent.

One-dimensional wave equation for some amplitude $A(x,t)$

$$\frac{\partial^2 A}{\partial t^2}-v^2\frac{\partial^2 A}{\partial x^2}=0$$

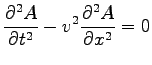
with the positive dispersion velocity $v$ is hyperbolic ($a=1$ , $b=0$ , $c=-v^2$ , $D_{\lambda}=4v^2>0$ ). Hyperbolic PDEs describe time-dependent, conservative processes, such as convection, that are not evolving toward steady state.

The next example is a diffusion equation for the patricle's density $\rho(x,t)$

$$\frac{\partial \rho}{\partial t}=D\frac{\partial^2 \rho}{\partial x^2},$$

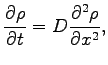
where $D>0$ is a diffusion coefficient is parabolic ($a=-D$ , $b=c=0$ , $D_{\lambda}=0$ ). Parabolic PDEs describe time-dependent, dissipative processes, such as diffusion, that are evolving toward steady state.

We shall consider each of these cases separately as different methods are required for each. The next point to emphasize is that as all the coefficients of the PDE can depend on $x$ and $y$ this classification concept is local.