wird gezeigt, daß sich die Koeffizienten einer
Taylorentwicklung der effektiven Hamiltonfunktion als
Felderwartungswerte ergeben. Diese Erwartungswerte kann man nun mit Hilfe von
MC-Simulationen ermitteln. Das Blockspinfeld , um das
die Hamiltonfunktion entwickelt wird, muß während der gesamten Simulation
fixiert sein. Nach dem Wilson'schen RG-Konzept erwartet man, daß das
simulierte System mit fixiertem Blockspin keine kritischen Fluktuationen aufweist,
sondern daß es nur noch kurzreichweitige
Fluktuationen in der Größenordnung einer Blocklänge besitzt.
Deshalb sollten selbst MC-Algorithmen mit
einem lokalen Update keine Probleme mit dem ``critical slowing down'' haben.
Dieses gilt aber nur, solange man nicht zu große Blöcke verwendet. Durch
die Gruppeneigenschaft der RG ist es möglich, einen Schritt mit großen Blöcken
in mehrere kleinere zu zerlegen, die man hintereinander ausführt. Das setzt
voraus, daß man die effektive Hamiltonfunktion durch einen überschaubaren Satz
von Kopplungen parametrisieren kann. Ebenso darf die Berechnung der effektiven Hamiltonfunktion
für eine Feldkonfiguration
nicht zu aufwendig sein, um
weitere Simulationen mit dieser effektiven Theorie zu ermöglichen.
Um die Algorithmen nicht von vornherein auf das Sine-GORDON-Modell festzulegen,
soll eine erweiterte Klasse von Hamiltonfunktionen eingeführt werden.
Bestandteile sind die Wechselwirkung einer freien, masselosen Theorie
und ein Potential .
Die Hamiltonfunktion sei durch
gegeben.
Für die Taylorkoeffizienten müssen nach Gleichung (
)
Erwartungswerte der Form
gemessen werden. Erster Schritt wird ein Wärmebad-Algorithmus sein, der Feldkonfigurationen mit der Verteilung
generiert. Dazu berechnet man die bedingte Wahrscheinlichkeitsverteilung für
einen Spin , wenn man alle anderen konstant hält,
mit und
. Damit ist
normalverteilt, und ein Single-Spin-Update kann mit Standardroutinen durchgeführt werden.
Anschließend wird diesem Spin-Update mit Hilfe eines Metropolis-Filters das
Potential aufgeprägt. Dazu faßt man den Spin-Update des
Wärmebad-Algorithmus als Testschritt auf, den man nur dann annimmt, wenn
wobei eine Zufallszahl sein soll und die Wahrscheinlichkeitsverteilung von
einer Gleichverteilung
auf dem Intervall
entsprechen soll.
Für ein solches Update kann zum einen die Berechnung der
Potentiale, zum anderen die Auswertung des Terms
bei nichtlokalen kinetischen Termen zeitaufwendig sein.
Um diese Summation zu optimieren, muß man bei den verwendeten RISC-Prozessoren
darauf achten, daß ihre Pipelines nicht ``leer laufen''. Dies erreicht man
durch eine lineare Adressierung des Feldes.
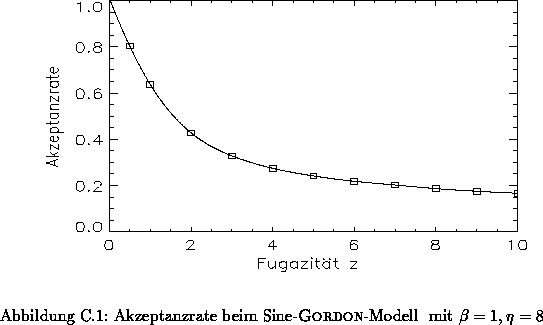
Problematisch ist dieser Algorithmus, wenn das Potential groß gegenüber dem kinetischen
Term wird. Abbildung beschreibt die Akzeptanzrate des
Wärmebad-Updates durch den Metropolis-Filter. Man erkennt, daß für große Fugazitäten
dieser Algorithmus weniger geeignet ist, da zu viele Vorschläge vom
Metropolis-Filter abgelehnt werden. Für große Fugazitäten ist es deshalb sinnvoller,
den Updater zur Verteilung () als reinen Metropolis-Algorithmus zu konzipieren.
In dieser Arbeit werden
die RG-Flüsse nur für kleine Fugazitäten betrachtet, so daß dieses
Problem (mit Ausnahme von MC-Simulationen zu Abschnitt ) nicht auftrat.