Näherungsverfahren in der modernen Physik

Mi 15-17, AP, SR 222
Amiranashvili, S.
Purwins, H.-G.

NÄHERUNGSVERFAHREN sind notwendig, weil exakte Lösungen in der Physik und in der Technik selten sind. Näherungslösungen können analytisch, numerisch oder eine Kombination aus beiden sein. In diesem Kurs lernen Sie, wie man analytische Näherungen findet.

Die Hauptthemen

• Qualitative Methoden und Dimensionsmethoden. Wie man ein Problem löst, ohne es wirklich zu lösen.
• Asymptotische Entwicklungen. Das sollten Sie zuerst versuchen, wenn Sie eine Gleichung mit einem kleinen Parameter haben.
• Methode der stationären Phase. Wie man schwierige Integrale behandelt.
• Störungstheorie. Wie man neue Resultate durch kleine Störung aus den Alten erhält.
• Methode der Skalentrennung. Entsprechend Nayfeh wird sie alle sechs Monate wiederentdeckt.
• Methode der Mittelwertbildung. Ein Spezialfall der Skalentrennung. Jedoch ist sie so populär, dass sie einen eigenen Namen hat.

ANMERKUNGEN. In der Regel nehmen wir konkrete Probleme und zeigen, wie man sie löst, anstatt eine allgemeine Theorie zu entwickeln. Der Kurs richtet sich an Studierende nach den Vordiplom.

Drei typische Probleme

1. Können Sie diese Gleichung
   
   für kleine 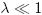oder große 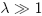lösen?
2. Warum ist 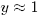eine schlechte Näherungslösung der Differentialgleichung
   
   sogar für kleine
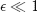
3. Warum ist es so schwierig Integrale, wie z.B.
   
   zu berechnen?

Literatur:

A. H. Nayfeh, Perturbation methods, Wiley 1973.