Netzwerkanalyse mit dem Knotenpotentialverfahren

Wir betrachten das Beispiel aus der Vorlesung

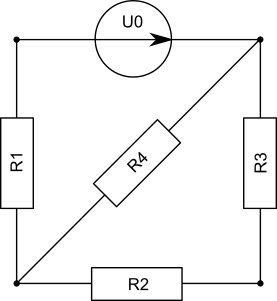
und nummerieren die Knoten ab 0 durch. Mit Hilfe des Knotenverfahren können wir folgendes Gleichungssystem aufstellen

\[\begin{split}\left( \begin{array}{ccccc} 0 & 0 & 0 & -R_3 & -R_4 \\ R_1 & -R_2 & 0 & 0 & R_4\\ -1 & 0 & 0 & -1 & 0\\ 0 & -1 & 0 & 1 & 1\\ 0 & 1 & 1 & 0 & 0 \end{array} \right)\cdot \left( \begin{array}{ccccc} I_0\\I_1\\I_2\\I_3\\I_4 \end{array} \right) = \left( \begin{array}{ccccc} -U_0\\0\\0\\0\\0 \end{array} \right)\end{split}\]

In Python greifen wir in dieser Vorlesung zunächst auf die NumPy Bibliothek zurück:

import numpy

Diese erlaubt es uns Vektoren und Matrix anzulegen und mit diesen zu operieren.

Knotenpotentiale und Spannung hängen linear zusammen, so dass wir dies als Matrix A schreiben können:

R1 = 1; R2 = 2; R3 = 5; R4 = 1
A = numpy.array([[0,    0, 0, -R3, -R4],
                 [R1, -R2, 0,   0,  R4],
                 [-1,   0, 0,  -1,   0],
                 [ 0,  -1, 0,   1,   1],
                 [ 0,   1, 1,   0,   0]])

und ausgeben:

print A

wobei wir konkrete Werte für \(R_i\) ansetzen mussten. Weiter ist in obigem Beispiel die Spannung gegeben, welche zwischen Knoten 1 und 2 (in Masche 0) anliegt:

U0 = 10
b = numpy.array([-U0, 0, 0, 0, 0])

die Werte des arrays müssen bei Zuweisung bekannt sein, so dass wir hier nicht, wie an der Tafel eine Funktion in Abhängigkeit der Zeit einsetzen können.

Nun können wir für diese Konkrete Wahl die Potentiale an den Knoten 0 bis 4 berechnen als:

I = numpy.linalg.solve(A,b)
print I

Download 02-netzwerk.py