Contents
%%Herleitung des LR-Algorithmus %Aufgabe: Bestimme alle Eigenwerte und Eigenvektoren einer Matrix.
Beispiel: 4x4
Definition der symmetrischen Matrix, Eigenwerte, Eigenvektoren
n=4;
A=rand(n); A=A+A'
[Eigenvektoren,Eigenwerte]=eig(A);
Eigenwerte=diag(Eigenwerte)';
[B,I]=sort(abs(Eigenwerte),'descend');
Eigenwerte=Eigenwerte(I); Eigenvektoren=Eigenvektoren(:,I);
D=diag(diag(Eigenvektoren)); Eigenvektoren=Eigenvektoren*inv(D);
Eigenwerte
Eigenvektoren
A =
0.6761 1.1706 0.1661 1.4510
1.1706 1.8866 1.2546 0.8833
0.1661 1.2546 0.8650 0.4127
1.4510 0.8833 0.4127 1.5070
Eigenwerte =
4.1092 1.3345 -0.6391 0.1302
Eigenvektoren =
1.0000 -0.8037 2.1983 -0.6942
1.4015 1.0000 -1.0847 -1.1328
0.7396 1.2341 1.0000 1.5295
1.1507 -1.3127 -1.2321 1.0000
Potenzmethode
Klassische Potenzmethode zur Bestimmung des Eigenvektors. 10 Iterationen zu zufälligem Startvektor.
x0=rand(n,1) xn=x0; for i=1:10 xn=A*xn; xn=xn/xn(1); end xn
x0 =
0.8360
0.2537
0.5344
0.4352
xn =
1.0000
1.4015
0.7396
1.1507
Potenzmethode zu mehreren Startvektoren
Idee: Wir führen die Potenzmethode auf mehreren Startvektoren durch.
X=rand(n,n); for i=1:4 X=A*X; X=X*inv(diag(X(1,:))); if (i<5) X end end X % Kein befriedigendes Ergebnis - alle Vektoren sind gleich.
X =
1.0000 1.0000 1.0000 1.0000
2.3081 1.7882 1.6346 1.6979
1.4576 0.8237 0.9347 0.8989
1.1666 1.4227 1.1658 1.2425
X =
1.0000 1.0000 1.0000 1.0000
1.5781 1.3750 1.4554 1.4297
0.9043 0.7462 0.7904 0.7770
1.1010 1.1094 1.1355 1.1253
X =
1.0000 1.0000 1.0000 1.0000
1.4644 1.4134 1.4214 1.4196
0.7919 0.7450 0.7561 0.7531
1.1419 1.1558 1.1479 1.1505
X =
1.0000 1.0000 1.0000 1.0000
1.4204 1.4021 1.4075 1.4059
0.7561 0.7409 0.7448 0.7437
1.1468 1.1494 1.1494 1.1494
X =
1.0000 1.0000 1.0000 1.0000
1.4204 1.4021 1.4075 1.4059
0.7561 0.7409 0.7448 0.7437
1.1468 1.1494 1.1494 1.1494
Konvergenzverhinderung
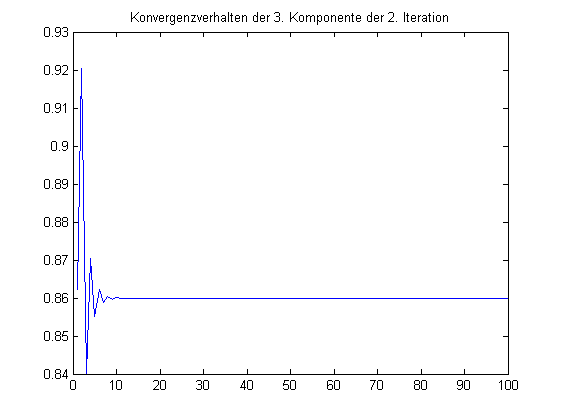
Neue Idee: Verhindere in der zweiten Folge die Konvergenz gegen den ersten Eigenvektor. Ziehe ein geeignetes Vielfaches des aktuellen Glieds der ersten Folge ab, so dass die erste Komponente 0 wird, und normiere die zweite Komponente.
X=rand(n,2); disp=zeros(100,1); for i=1:100 X=A*X; X(:,2)=X(:,2)-X(1,2)/X(1,1)*X(:,1); X=X*inv(diag(diag(X))); disp(i)=X(3,2); if (i<5) X end end plot(disp) title('Konvergenzverhalten der 3. Komponente der 2. Iteration');
X =
1.0000 0
1.3236 1.0000
0.6419 0.8622
1.1806 0.0374
X =
1.0000 0
1.3636 1.0000
0.7093 0.9204
1.1530 -0.2482
X =
1.0000 0
1.3909 1.0000
0.7300 0.8400
1.1532 -0.1497
X =
1.0000 0
1.3977 1.0000
0.7364 0.8704
1.1512 -0.1982
Erweiterung auf n Folgen
Diese Idee läßt sich auf n Folgen übertragen: Ziehe in der n. Folge ein geeignetes Vielfaches der aktuellen Glieder der 1. bis (n-1). Folge ab, so dass die Komponenten 1 bis n-1 verschwinden, und normiere die n. Komponente.
X=rand(n,n); for i=1:4 X=A*X; for j=1:n for l=1:j-1 X(:,j)=X(:,j)-X(l,j)/X(l,l)*X(:,l); end end for j=1:n X(:,j)=X(:,j)/X(j,j); end X end % Die X_k sind linke untere Dreiecksmatrizen. Nach der Herleitung hoffen % wir: X_k konvergiert gegen XR, wobei X die Matrix der Eigen- und % Hauptvektoren von A ist.
X =
1.0000 0 0 0
1.8326 1.0000 0.0000 -0.0000
1.1881 0.9112 1.0000 0
1.0038 -0.1709 -2.2660 1.0000
X =
1.0000 0 0 0
1.5653 1.0000 0 -0.0000
0.8731 0.8639 1.0000 0
1.1335 -0.1800 -1.3923 1.0000
X =
1.0000 0 0 0
1.4472 1.0000 0 0
0.7801 0.8591 1.0000 -0.0000
1.1405 -0.1804 -1.5562 1.0000
X =
1.0000 0 0 0
1.4170 1.0000 0 0
0.7527 0.8606 1.0000 0.0000
1.1481 -0.1835 -1.5238 1.0000
LR-Verfahren
Im LR-Verfahren betrachten wir die Matrizen
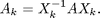
Sie sind alle ähnlich zu A und konvergieren gegen eine rechte obere Dreiecksmatrix. Zur Berechnung kann man die LR-Zerlegung verwenden:
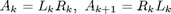
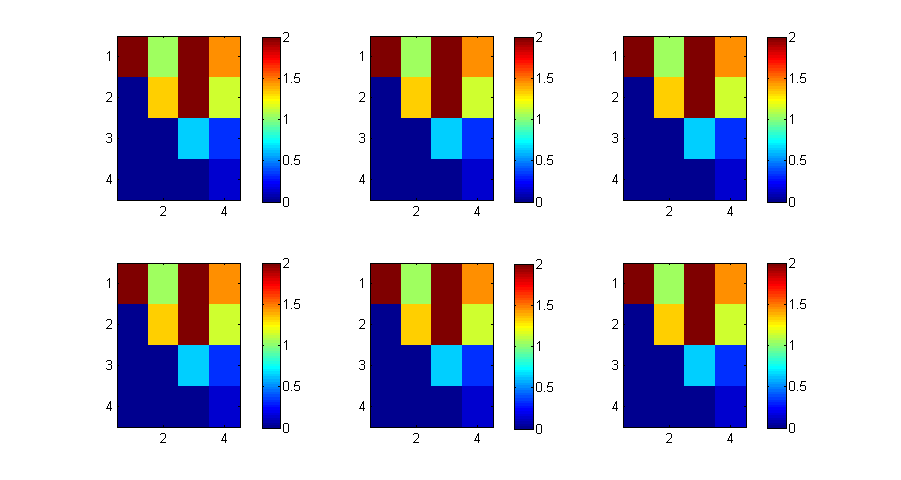
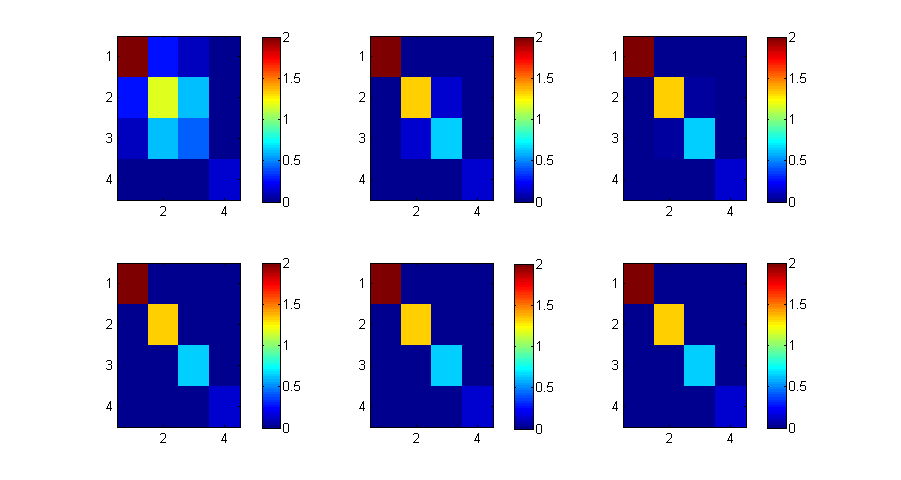
Beispiel mit 48 Iterationen. Bild alle 6 Iterationen.
close figure('Position',[1 1 900 480]) X=A; P=8; for i=1:P*6 [L,R]=lu(sparse(X),0); X=R*L; if (mod(i,P)==0) subplot(2,3,i/P); imagesc(abs(X),[0 2]); colorbar; end end full(diag(X))'
ans =
4.1092 1.3345 -0.6391 0.1302
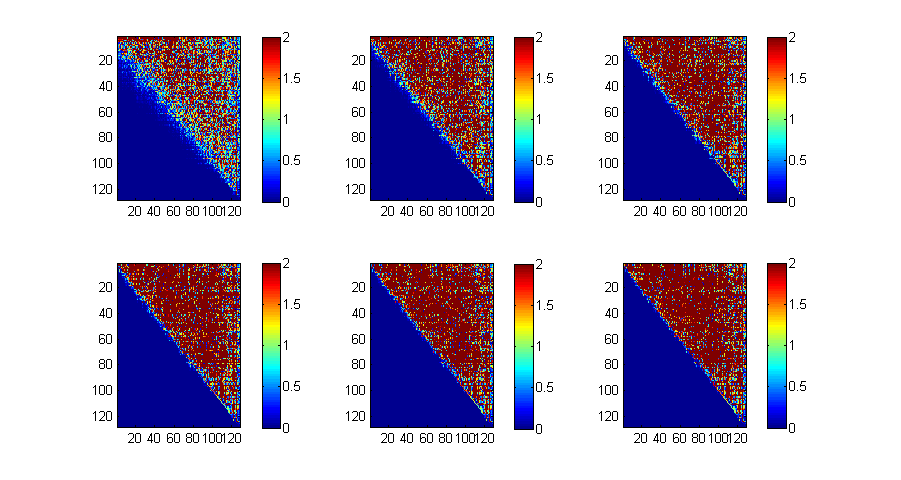
LR-Verfahren mit grosser Matrix
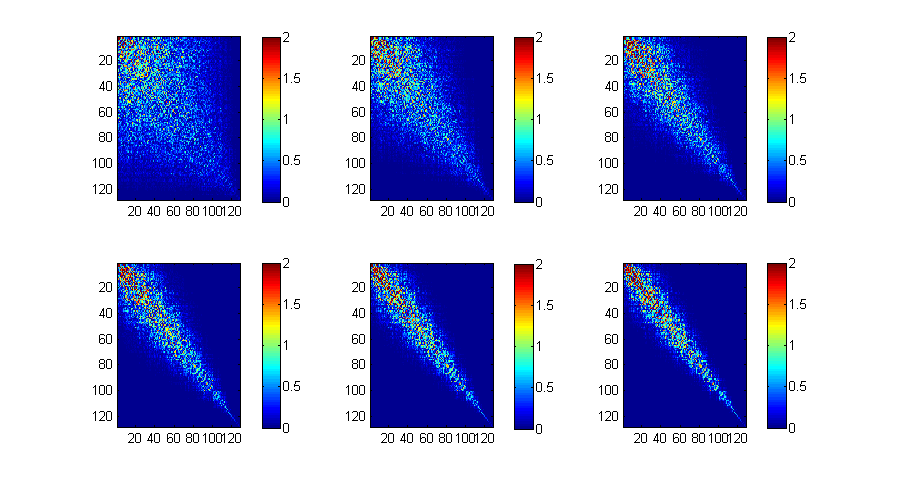
Gleiches Beispiel wie oben, aber mit einer 128x128-Matrix und 96 Iterationen.
X=rand(128,128); X=X+X'; P=16; for i=1:P*6 [L,R]=lu(sparse(X),0); X=R*L; if (mod(i,P)==0) subplot(2,3,i/P); imagesc(abs(X),[0 2]); colorbar; end end
Alternative: Konvergenzverhinderung durch Orthogonalität
Idee hier: Wähle die erste Folge so, dass alle Iterierten die Norm 1 haben. Addiere bei der zweiten Folge ein Vielfaches der ersten, so dass alle Iterierten der zweiten Folge senkrecht auf denen der ersten stehen usw.
close X=rand(n,2); disp=zeros(100,1); for i=1:100 X=A*X; X(:,1)=X(:,1)/sqrt(X(:,1)'*X(:,1)); X(:,2)=X(:,2)-(X(:,1)'*X(:,2))*X(:,1); X(:,2)=X(:,2)/sqrt(X(:,2)'*X(:,2)); disp(i)=X(3,2); if (i<5) X end end % Problem: Die X_k haben wieder eine Darstellung der Form XR_k, aber % diesmal konvergieren die R_k nicht.
X =
0.4093 -0.4233
0.6447 0.2605
0.3130 0.7629
0.5647 -0.4135
X =
0.4640 -0.3790
0.6309 0.4423
0.3367 0.5792
0.5228 -0.5703
X =
0.4543 -0.3597
0.6371 0.4497
0.3348 0.5626
0.5250 -0.5932
X =
0.4552 -0.3650
0.6370 0.4533
0.3361 0.5575
0.5236 -0.5920
QR-Verfahren
Wir betrachten wieder
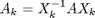
Dann lassen sich die A_k einfach berechnen durch die QR-Zerlegung:
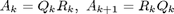
6 Iterationen.
close figure('Position',[1 1 900 480]) X=A; P=2; for i=1:P*6 [Q,R]=qr(X); X=R*Q; if (mod(i,P)==0) subplot(2,3,i/P); imagesc(abs(X),[0 2]); colorbar; end end diag(X)'
ans =
4.1092 1.3345 -0.6391 0.1302
QR-Verfahren - grosse Matrix
Beispiel: 128x128-Matrix, 16 Iterationen.
X=rand(128); X=X+X'; P=2; for i=1:P*6 [Q,R]=qr(X); X=R*Q; if (mod(i,P)==0) subplot(2,3,i/P); imagesc(abs(X),[0 2]); colorbar; end end