The backprojection (i.e. Step 2 in Algorithms 1-3) is the most time consuming part of the
filtered backprojection algorithm. The filtering or convolution step (Step 1 in Algorithms 1-3) requires in principle the same number of operations, but this can easily be reduced drastically either by cutting off the filter 
or by using the fast Fourier
transform (FFT).
The backprojection consists is the evaluation of the sums
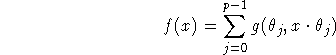
on a 
grid. This is the simplest case of Algorithm 1, the resolution of the image being adjusted to the number of views p according to the sampling theorem. Nilsson
(1997) suggested a devide and conquer strategy for doing this with O 
operations, as opposed to the O 
operations of a direct evaluation. Suppose 
.
Step 1: For 
compute
Since 
is constant along the lines 
it suffices to compute 
at 2p points x. We need 
operations.
Step 2: For 
compute
Since , 
are constant along the lines , 
, respectively, 
is almost constant along the lines 
where 
.
Hence it suffices to compute only for a few, say 2, points on each of those lines.
This means that we have to evaluate at 4p points, requiring 
operations.
Step 3: For 
compute
With the same reasoning as in step 1 and 2 we find that it suffices to compute 
for only for 8p points, requiring 
operations.
Proceeding in this fashion we arrive in step m at the approximation 
to f,
which has to be evaluated at 
points. Hence the number of operations in step 1 to m
is
and this is O . Of course this derivation is heuristic, and we simply ignored the necessary interpolations and approximations. But practical experience demonstrates that such an algorithm can be made work.