e. What are the free energy and the chemical potential?

 

Most of us learned at school, that every physical system tends to minimize its energy. But this is not correct; at least it’s not the whole truth. In reality a many body system tries to decrease its energy and additionally tries to reach a state with maximum disorder. So physicists introduced the so called “free energy”

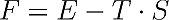
Where F denotes the “free energy”, E the “normal energy”, T the temperature and S the entropy. The entropy is a measure of disorder where entropy 0 means total order in e.g. a perfect crystal at zero Kelvin; higher values of the entropy represent a higher state of disorder.

Now statistical mechanics, quantum as well as classical, says that a system always tries to minimize its free energy instead of minimizing the energy or maximizing the entropy. When the system reaches a minimum of the free Energy it is in thermal equilibrium. This means that the system has reached a stationary state, where all his macroscopic variables don't change in time as long as the system is isolated. In most cases a decrease in energy leads also to an decrease in disorder. So we have a competition between minimizing energy and maximizing disorder. 

Lets first look at a process in which the energy and disorder of a system is decreased. As long as the energy decrease compensates the decrease in disorder the "free Energy" will also decrease. Hence it is a spontanous process which happens without external influence as it helps to minimize the "free energy". For example:

When a paramagnetic material makes the transition into the ferromagnetic state it significantly increases its order. Before all elementary magnetic moments were oriented arbitrarily in space, while in the ferromagnetic phase they are all aligned parallel to each other within one magnetic domain. But on the other hand the material reduces also its inner energy, as the dipolar energy depends on the distance between neighboring north and south poles of the elementary magnetic moments which is minimized in the parallel configuration. That’s the reason why some materials make a transition into the ferromagnetic state below a certain temperature; they try to minimize their free energy. In most materials the reduction of internal energy is not sufficient to justify the highly ordered ferromagnetic state. Those materials never become ferromagnetic, although they have elementary magnetic moments in them; these materials then always stay paramagnetic.

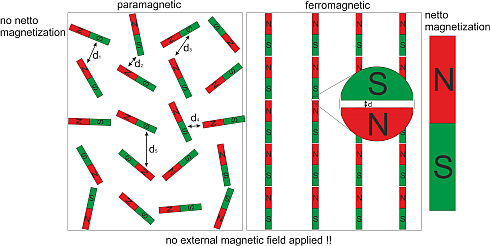
The other way around is also realized in ferromagnets. A ferromagnetic material can decrease its order significantly by producing magnetization waves (also called spin waves) which increase the inner energy of the ferromagnet just a little. I will point this out later.

In conclusion, every many particle system tries to reduce its free energy. The state of a gas in which the free energy is minimized is called thermal equilibrium. As long as we do not change any external parameter, like temperature, pressure etc. a many particle system once reached will stay in thermal equilibrium.

Another important property of quantum many particle systems concerning Bose-Einstein condensation is the chemical potential. The chemical potential is defined for a system in thermal equilibrium. It declares by how much the free energy of a system in thermal equilibrium will change when we add one additional particle into the system.

In a system where the particle number stays constant over time, e.g. in a gas of atoms the chemical potential will take an arbitrary value depending on the parameters (temperature, pressure) of the gas.

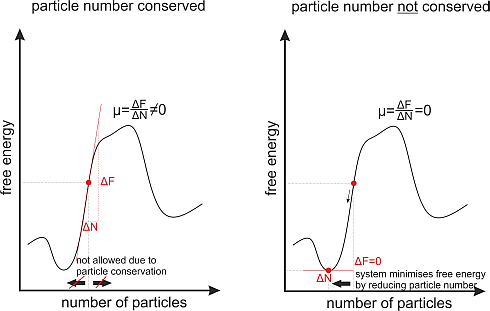
But there are also systems where the particle number is not constant over time, for example photons in a black body. A black body is a closed box with black walls. These walls absorb every photon that hits them and they create photons by themselves, at room temperature mainly infrared photons due to heat radiation. In such a system the number of photons is not conserved, as they are destroyed and created all the time.

Consequently the chemical potential is always zero in thermal equilibrium. The reason for this is very simple. As the number of particles in the system is variable now, the system will choose the particle number in such a way that the free energy is minimized. And as we know from mathematics in school; the slope of a function at its minimum is always zero.

The operative point now is, that destruction or creation of particles always takes some time and doesn’t happen instantly. This opens up a way to raise the chemical potential in a system where the particle number is not conserved. We will see later, that this is a crucial step in the creation of a magnon Bose Einstein condensate.

Now since the "free energy" and the chemical potential where introduced, the next section deals with the question:

What are the distribution functions in many body systems?