d. What are Magnons?

 

I already addressed that in quantum mechanics waves can, under certain conditions, be described as particles. Light is a good example. Light is an electromagnetic wave consisting of oscillating electric and magnetic fields. The corresponding particle is the photon it carries the energy

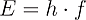
and propagates with the speed of light

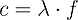
with h Planck’s constant, λ the wavelength and f the frequency of the light wave. The spin of a photon is one therefore it is a Boson.

The elementary particle of a spin-wave is called a Magnon. Like a Photon a Magnon carries the energy

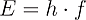
where f is the precession frequency of the individual spins in a spin wave. They carry a spin equal to one. Magnons can be imagined as one complete precession distributed over a chain of spins.

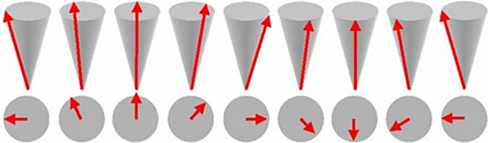
The velocity distribution of such magnons is indeed not as simple as that of photons. The velocity of a photon in free space does not depend on propagation direction and frequency. On the contrary, the velocity of magnons depends on the angle between propagation direction and external magnetic field and on precession frequencies of the individual spins building up the magnon.

In the following sections I will mostly use the term magnon, especially when talking about statistics. If the wave properties of the magnon are important I will use the term spin-wave. Physically both are two sides of one coin; didactically it is often useful to distinguish between them.

It should be kept in mind, that the statement:

A spin wave has frequency f and a magnon has energy E are equivalent, as the energy of a magnon can be calculated via

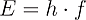
and vice versa.

In the first chapter I introduced some basic consecpts of Bose Einstein Kondensation. In this chapter basic concepts of Spin Waves and Magnons were treated. Thereby the foundation for a basic understanding of

Magnon Bose Einstein condensation

should exist.