Implementation of the Thin-Film Equation on Prestructured, Switchable Substrates Using the oomph-lib Library
created by Janik Suer, Moritz Stieneker, Svetlana Gurevich, and Simon Hartman

• Droplet coalescence simulation using Swalbe.jl
  created by Stefan Zitz & Jens Harting

 

• Overview of available auto07p Tutorials 
  The text briefly introduces the "Münsteranian Torturials on Nonlinear Science", a series of hands-on tutorials on the practical application of numerical path-continuation methods for problems in soft matter and pattern formation. A recommended sequence of working through the tutorials is laid out and for each tutorial an abstract is given.
• Steady drop and film states on a horizontal homogeneous substrate

  

  This tutorial explores an equation for steady drop-and-hole solutions derived from the dimensionless thin film (or lubrication) equation. You will calculate steady solution of the equation by continuation in a number of different control parameters (domain size, mean height).

• Sliding drops modelled by a thin film equation for a liquid layer or drop on an inclined homogeneous substrate

  

  In this tutorial a dimensionless thin film equation closely related to the one in DROP is used. In this case a lateral driving force is included and solutions for sliding drops on an inclined plane are examined. You will calculate steady solutions [in the comoving frame], in particular, drops moving at a constant velocity. The main treated control parameter is the inclination angle.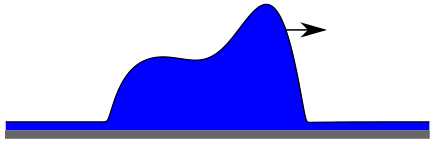
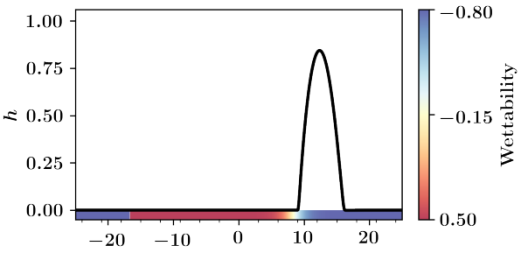
• Steady states of a thin film equation for a liquid layer or drop on a horizontal heterogeneous substrate

  

  In this tutorial the dimensionless thin film equation used in the tutorial DROP is adapted to a substrate of varying wettability. In particular, the long-range contribution of the disjoining pressure is sinodally modulated. You will calculate steady solutions and their bifurcations that emerge when using the heterogeneity strength as control parameter.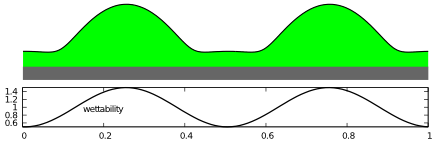

• Linear stability of steady solutions of a thin film equation for a horizontal homogeneous substrate

  

  This tutorial calculates the same steady solutions as the tutorial DROP but this time together with their (1d and 2d) linear stability with respect to time-dependent perturbations. You will calculate a dispersion relation (growth rate over transversal wave number) and continue solutions and their stability in various parameters.

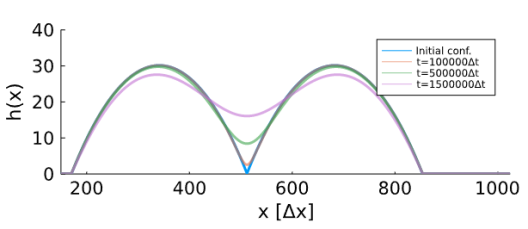
• Steady drops on a heterogeneous substrate under lateral driving
  This tutorial explores steady drops on a surface with heterogeneous wettability under the influence of lateral driving. You will calculate these steady states as a function of continuation parameters: domain length, heterogeneity strength and driving parameter.

 

• Linear stability of sliding drops on an inclined homogeneous substrate 
  The tutorial employs continuation techniques to calculate selected stationary states of a driven thin-film equation together with their linear stability, i.e., steady profiles, their eigenvalues and eigenfunctions are continued in parallel.

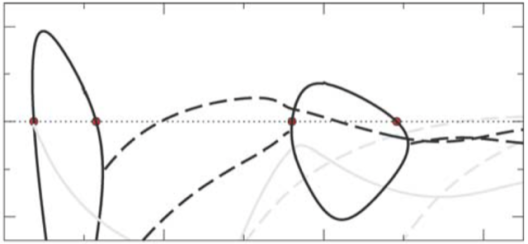
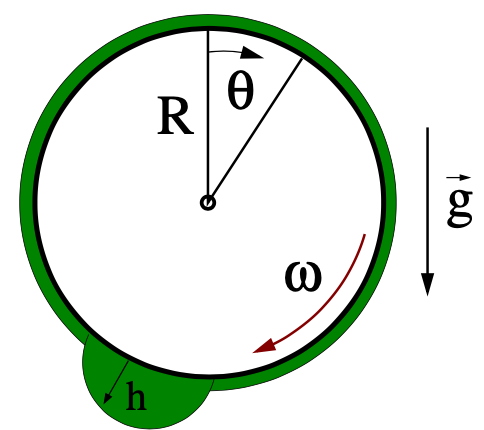
• Steady and time-periodic states of drops on a rotating cylinder 
  The tutorial employs continuation techniques to calculate steady and time-periodic drop states on a rotating cylinder.  You will investigate depinning transitions that occur when the rotation speed of the cylinder is increased similar to the depinning of drops on heterogenous substrates.